Algoritma Minimax Pada Game Tic-Tac-Toe Android

June 28, 2018

Apa itu MiniMax

Minimax merupakan suatu algoritma yang digunakan pada pembuatan keputusan dan game theory. khususnya zero-sum game yang dijalankan oleh dua pemain secara bergantian, algoritma ini mencoba untuk mencari langkah yang paling optimal untuk pemain untuk bisa memenangkan permainan, dengan asumsi bahwa lawan juga bermain secara optimal. contoh game ini seperti Tic-Tac-Toe, Backgamon, Catur dsb.

Pada suatu game, algoritma ini akan menganggap kedua pemain pada game yang disebut maximizer dan minimizer. maximizer mencoba untuk mendapatkan nilai tertinggi, sementara minimizer sebaliknya mendapatkan nilai yang terendah untuk mengimbangi maximizer.

Artikel ini akan membahas tentang game tic-tac-toe, setiap state pada game, dan setiap langkah yang memungkinkan memiliki suatu nilai, dimana nilai tersebut dikalkulasikan secara rekursif sampai ke state akhir/terminal game. untuk maximizer agar bisa menang maka nilai yang ingin dia temukan adalah suatu nilai maximum yang merepresentasikan bahwa itu adalah langkah yang optimal, sementara minimizer sebaliknya langkah optimal untuk memenangkan permainannya adalah dengan nilai yang rendah.

Tic-Tac-Toe Game

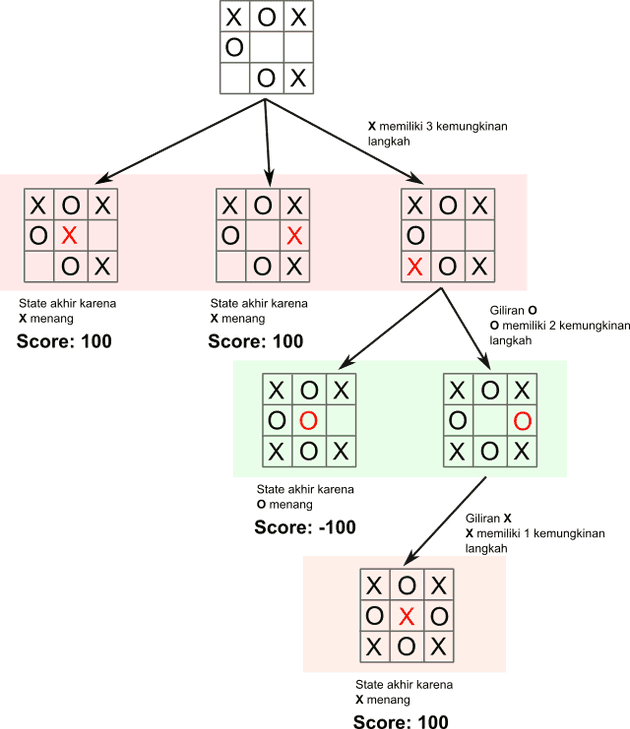
Asumsi pada state game tic-tac-toe terdapat dua pemain X dan O, dimana X adalah maximizer player yang mencari nilai max dan O adalah minimizer player yang mencari nilai min, state permain digambarkan oleh node root (paling atas), dan pada saat itu adalah giliran X.

Nilai 100 diberikan jika X menang.
Nilai -100 diberikan jika O menang (X kalah).
0 jika seri.

Pada game state seperti node root diatas maka X akan memiliki 3 kemungkinan langkah yang dapat diambil karena X adalah maximizer maka dua state pertama yang menghasilkan end/terminal state yang menjadikan X menang akan dipilih (salah satu).
Tetapi jika asumsi X memilih langkah ketiga maka dia tidak akan memenangkan game pada saat itu dan gilirian selanjutnya adalah O.
O memiliki 2 kemungkinan langkah yang dapat diambil, tentunya karena O adalah minimizer maka dia akan memilih langkah pertama yang merupakan terminal state dan menjadikannya pemenang game dengan nilai -100.
Tetapi jika dievaluasi lebih lanjut untuk langkah O yang kedua maka tidak akan menjadikannya menang, sehingga masuk kegiliran selanjutnya yaitu X dimana hanya ada satu cell yang dapat diisi dan menjadikannya (X) menang dengan nilai 100.

Koding

Project android tersedia di repo github ini

Papan tic-tac-toe

Papan tic-tac-toe merupakan grid dengan jumlah 9 cell, dapat direpresentasikan menggunakan array 1 atau 2 dimensi, disini akan digunakan array 1d dengan jumlah element 9 dari index 0 - 8.

const val BOARD_SIZE = 3
const val EMPTY_TOKEN = 0
private const val ARRAY_SIZE = BOARD_SIZE * BOARD_SIZE

class Board(val data: IntArray = IntArray(ARRAY_SIZE, { EMPTY_TOKEN })) {

    init {
        if (data.size != ARRAY_SIZE) {
            throw IllegalArgumentException(
                    "data array size must have exactly $ARRAY_SIZE elements, current size ${data.size}")
        }
    }

    val isFull: Boolean
        get() {
            for (cell in data) {
                if (cell == EMPTY_TOKEN) return false
            }
            return true
        }

    operator fun get(i: Int) = data[i]
    operator fun set(i: Int, newValue: Int) {
        data[i] = newValue
    }
}

Langkah tic-tac-toe

Buat class untuk merepresentasikan langkah-langkah yang dapat diambil pada game dimana nantinya akan digunakan oleh algorithma minimax untuk di kembalikan.

data class Move(
        val index: Int = -1,
        val score: Int = 0
) {
    val isValid inline get() = index >= 0
}

Fungsi skor (evaluation function)

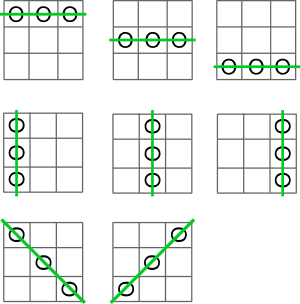
Ini merupakan suatu fungsi yang digunakan untuk mengetahui apakah ada formasi menang (tiga baris token yang sama berturut-turut) untuk suatu pemain atau tidak, pengecekan berlangsung untuk setiap cell secara horizontal, vertical dan diagonal.

Jika misalkan player maximizer menang maka akan dikembalikan suatu nilai maximum (misal 100) sebaliknya jika minimizer menang kembalikan nilai minimum (misal -100), tetapi jika tidak ada atau belum ada yang menang maka return nilai untuk menandakan seri/draw (misal 0).

class BoardEvaluator {
    companion object {
        const val VAL_MAX = 100
        const val VAL_MIN = -100
        const val VAL_DRAW = 0

        @JvmStatic
        fun evaluate(board: Board, maxPlayer: Int, minPlayer: Int): Int {
            // horizontal
            for (i in 0..6 step 3) {
                if (board[i] == board[1 + i] && board[1 + i] == board[2 + i]) {
                    if (board[i] == maxPlayer) return VAL_MAX
                    else if (board[i] == minPlayer) return VAL_MIN
                }
            }

            // vertical
            for (i in 0..2) {
                if (board[i] == board[3 + i] && board[3 + i] == board[6 + i]) {
                    if (board[i] == maxPlayer) return VAL_MAX
                    else if (board[i] == minPlayer) return VAL_MIN
                }
            }

            // diagonal
            if (board[0] == board[4] && board[4] == board[8]) {
                if (board[0] == maxPlayer) return VAL_MAX
                else if (board[0] == minPlayer) return VAL_MIN
            }

            if (board[2] == board[4] && board[4] == board[6]) {
                if (board[2] == maxPlayer) return VAL_MAX
                else if (board[2] == minPlayer) return VAL_MIN
            }

            return VAL_DRAW
        }
    }
}

Algoritma Minimax

Ini merupakan implementasi basic yang tidak memiliki tuning apaput, misalkan bisa saja ditambahkan parameter depth untuk menghitung atau membatasi kedalaman traversal tree yang dilakukan dsb. Algoritma ini memang cukup membingungkan pertama kali dan memang cukup sulit untuk didebug atau ditrace karena pemanggilan fungsi yang rekursif dengan jumlah yang cukup besar.

class GameAi(val maxPlayer: Int, val minPlayer: Int) {

    fun findBestMove(board: Board, player: Int): Move = minimax(board, player)

    private fun minimax(board: Board, player: Int): Move {
        val score = BoardEvaluator.evaluate(board, maxPlayer, minPlayer)
        // cek end state
        if (board.isFull || score == BoardEvaluator.VAL_MAX || score == BoardEvaluator.VAL_MIN) {
            return Move(score = score)
        }

        // iterasi cell yang kosong pada board
        val moves = ArrayList<Move>()
        for (i in 0 until board.data.size) {
            // skip jika cell tidak kosong
            if (board[i] != 0) continue
            board[i] = player
            // ganti player secara bergiliran
            val move = if (player == maxPlayer)
                minimax(board, minPlayer) else
                minimax(board, maxPlayer)
            board[i] = EMPTY_TOKEN
            moves.add(Move(i, move.score))
        }

        // ambil langkah max/min
        val bestMove = if (player == maxPlayer) {
            moves.maxBy { it.score }
        } else {
            moves.minBy { it.score }
        }
        return bestMove ?: Move()
    }
}

Fungsi findBestMove() merupakan public API untuk menyembunyikan implementasi minimax(). terdapat dua parameter untuk fungsi minimax(board: Board, player: Int).

Pertama evaluasi apakah pada saat itu state board merupakan terminal node (end game) jika score yang dikembalikan sama dengan value max/min berarti pada formasi board tersebut terdapat player yang menang (maximizer atau minimizer), jika didalam board tidak ada lagi cell yang kosong maka permainan memang berakhir (karena tidak ada lagi langkah yang bisa diambil).

Variable moves digunakan untuk menyimpan setiap langkah yang memungkingkan untuk diambil oleh player pada saat itu.

Iterasi dan skip setiap cell yang ada pada board jika tidak kosong. Jika kosong itu artinya dapat menjadi kemungkinan langkah yang bisa diambil.

Karena pada saat ini misalkan adalah giliran maximizer dan dia telah menandai board pada index yang kosong tersebut dengan dirinya, maka setelah itu adalah giliran minimizer dengan memanggil kembali fungsi minimax() (rekursif) dengan parameter player untuk player minimizer (begitu pula selanjutnya secara bergantian). Karena proses ini sama halnya seperti simulasi maka kosongkan kembali board pada index tersebut dengan menandainya menggunakan empty token (dalam hal ini EMPTY_TOKEN).

Jika proses iterasi sudah selesai dan kita memiliki list langkah-langkah yang dapat diambil (moves) maka tahap selanjutnya adalah menyaring langkah mana yang dianggap terbaik berdasarkan apakah player merupakan maximizer atau minimizer, jika maximizer maka ambil langkah dengan skor yang tertinggi (move.score), sebaliknya jika minimizer ambil yang terendah.